Levels of Organization

Why is a nation not just a soup of organic molecules?

DYSTOPIC ATTRACTOR corresponding to  increased resource flows and decreasing network connectivity as level goes up.

CHAOS ATTRACTOR-the colors represent distances from the central node, but the central node is completely arbitrary and hence there is no meaningful concept of intrinsic levels (there are extrinsic levels of an observer's coarse graining scale). Node connectivity is always the same.

THIRD ATTRACTOR? Corresponding to decreasing resource flows, unchanging connectivity per node, but decreasing connectivity to other levels, as level increases.

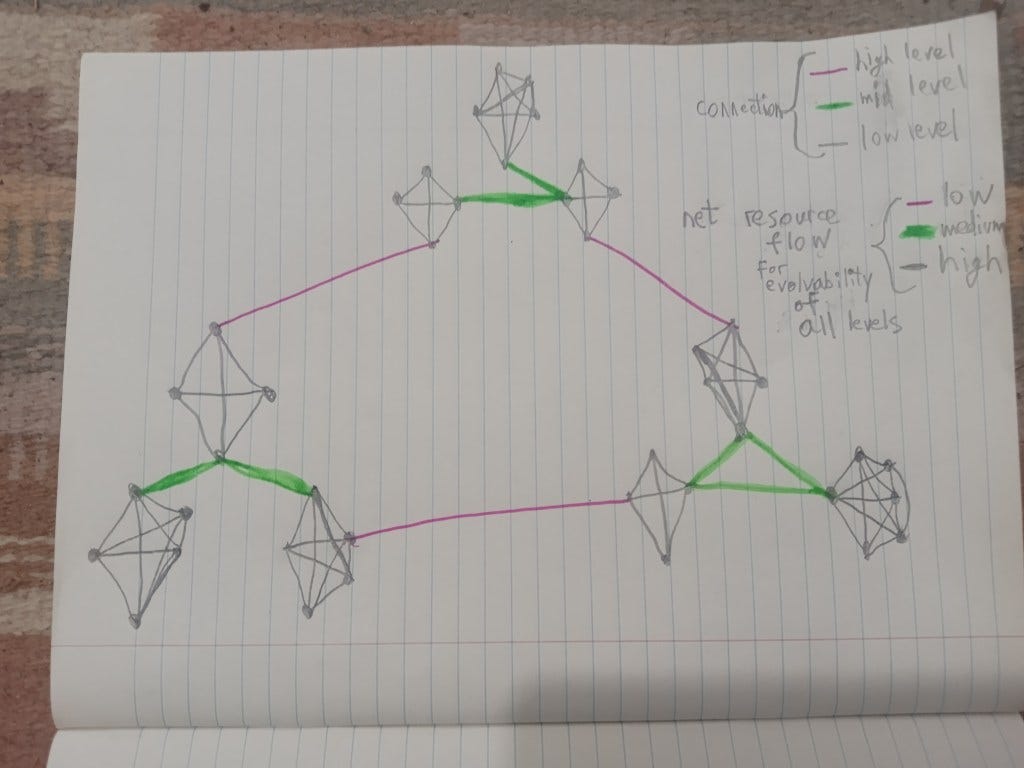
In this post I will try to make a connection between Daniel Schmactenberger’s (DS) 3 attractors, and levels of organization of living systems. Some of this is just a new way of looking at how resources flow in familiar systems, some of it is based on research, and some is speculative. DS talks about likely scenarios that civilizations tend towards. I believe these can be generalized to other living systems, and by doing so we gain insight into conditions that lead to each. DS invites us to think of conditions that lead to something that avoids the pitfalls of either the dystopic/totalitarian attractor, and the chaotic one, which he calls the third attractor. The dystopic attractor occurs in multicellular organisms because lower levels of organization (organs, cells, organelles) do not normally have any freedom, only the top level, the organism does. The chaotic attractor seems to occur in cases like cancer, where lower level parts (cells in the cancer case) are not able to be managed by the higher levels, and also acquire evolvability. I present 3 network diagrams that in addition to nodes and connections, also involve resource flows. Glance at them now to whet your appetite, and refer to them later as we discuss what they involve.

Functional levels

The simplest explanation to why a nation (and even more generally, life) is not just a soup of cells (or more drastically even, organic molecules), is a cost benefit analysis (I have thought of this, but probably many system theorists have thought of it before me) Technically, this latter what Terrence Deacon (see, for example, the book Incomplete Nature) calls “teleonomic” behavior, but it can get more complex in living system when the environment is represented and interpreted internally, to become what he calls “teleodynamic” behavior. To even talk about costs and benefits means that there is an entity that is optimizing a function, and this function can be split into increasing and decreasing tendencies, with regard to some variables. The function could be evolutionary fitness, but doesn’t have to be (as in the case of the thermostat) where it is just a difference between a present situation and a goal. For an entity to have a function, it implies optimization (or satisfaction, but satisficing is a special case of optimizing) of some mathematical utility function. Though cells inside a multicellular organism do not usually have their own fitness (unless they go cancerous), they do have a function, and hence are optimizing a utility function. There are benefits for cells to get together and specialize, and then to synergize their talents into a higher level like an organ (which confusingly, could also be called a primitive multicelular organism when this first evolved, as in primitive slime molds or bacterial colonies with no or minimal internal specialization). However, (according to the cost/benefit hypothesis) there are also costs to managing/coordinating these cells that increase faster than the benefits with the number of cells, and at a certain number of cells the costs catch up with the benefits. At this point a new level makes sense, so that marginal costs reset to zero above the level of organs and we get a multicellular organism with specialized organs. We will discuss this resetting to zero marginal costs in more detail in a future post and a bit here. It’s related to subsidiarity.

As the number of organs increases, there are benefits to synergizing different organs (with each having a specialized function), but the costs (communication, resource distribution, monitoring and punishing free riding) again increase faster with the number of organs and at a certain level we have a multicellular organism that can't handle the cost of managing more organs (even though their addition may provide benefits). At that point the costs above the individual level reset to zero, and a new level of family makes sense, etc. But why do the extra costs reset to near zero at each level as the number of parts at that level becomes one? Because the costs are (this is a hypothesis) to a first approximation proportional to the number of pairwise interactions (not the amount of resources flowing) and the most optimal arrangement (which is part of what we call proper nesting, we will look at extra requirements below with regard to evolvability of lower levels) is such that the number of these interactions is highest within a level, not across the level membrane. This affects the amounts of resources shared in a secondary manner. It seems to be the case (though I have not checked for actual data on this) that organelles share resources more within cells, not as much with other cells. Cells share resources more within organs, and not as much with cells of other organs. Organs share resources mostly in a body of a multicellular individual, and not as much with other individuals. In a properly nested arrangement (which we claim is NOT currently the norm in our culture, though it would be a way to get to the third attractor), human individuals share resources mostly within their family and not as much with individuals in other families, families share within their own clan more than other clans, etc. And there are representative parts at each level to do this commerce of resources; these parts are usually the membranes, transport proteins, and other mediating parts like limbs and mouths for multicellular organisms interacting with each other. The cell membrane mediates commerce between cells. The organ membrane mediates commerce between organs. Epithelial organs (skin, GI tract and respiratory for respiring organisms), as well as information gathering and transmitting organs like eyes, mouths and ears) mediate commerce between individual multicellular organisms. Prioritizing local commerce (at all levels down to organelles, not just between humans) over global commerce gets you this proper nesting for free, but there might be other ways to do it. The main point of this proper nesting of levels is to reduce the costs of commerce (by making it partially between levels as opposed to only horizontally between parts of a level), while not significantly affecting the benefits.

Besides the biological and social levels, we have cognitive levels: neurons, neural modules, personalities (which are not just coherent in 3D, but in 4D spacetime), and psychological individuals (which integrate and coordinate these lower levels/parts). We also have economic levels: large corporations that have sectors, departments, and teams. And corporations also have alliances and industry-organized collectives that promote their collective interests at higher levels. We do not know how functional these higher levels are compared to levels below multi-cellular organisms.

All these levels are functional levels. Functionality involves some agency, not just performing a function. It includes the ability to maximize a utility function some of whose variables are environmental and change without the control of the agent. Functionality without evolvability implies that the utility maximized is not the number of progeny (as happens with biological evolution), and the algorithm is not a genetic algorithm. There are many similarities between learning algorithms and Darwinian dynamics (which couples a genetic algorithm with ecological population equations) which we will discuss in future posts. You can look at this paper by Richard Watson for an explanation of learning algorithms. There are also some differences (not just similarities) that we think might be crucial for both emerging DS's third attractor, and for building a genuine Artificial General Intelligence.

Parts that have internal coherence and are specialized to do different jobs are called modular. Once they become specialized, modular parts can be coordinated into a new level by hiding their internal workings from other parts and coordinating them as coherent wholes, rather than through their own parts (though a few representative parts can be involved in the coordination, as we discussed above). In computer science this is called abstraction, in economics and governance it is called subsidiarity, and modularity/subsidiarity are necessary for emergence of a new functional level, without subsuming the previous lower level entities (if they actually are levels) into a collection of their sub-parts. Subsidiarity also insulates lower levels from an external environment by the higher levels, which is a benefit conferred on the lower levels by the higher levels when that environment is harsh.

Modularity and synergy of entities, precedes their abstraction into a coherent whole; for example when there are too many families in a village to manage (manage means both informationally and resource-wise, see below), the village can split into 2 or more villages, initially not specialized or synergizing. There is modularity of families as far as each village is concerned, with each family being a module, and there is abstraction of these modules into a village. But there is no abstraction yet of the different villages into a federation, because they have not yet achieved modularity/specialization (part of the definition of modularity is specialization). However, once there are enough villages, and these villages themselves become specialized and able to synergize, they can be abstracted into a higher level of a federation. We can see this sequence of modularity preceding synergy preceding abstraction at all levels, both social and biological. See if you can observe it at other levels than the 3 above (family, village and federation).

The abstraction of modules into a higher level is not guaranteed to happen. The synergistic benefits have to be higher than the costs of coordination and processing of information. In biological systems, besides informational costs and benefits, there are also energy and resource costs and benefits of abstraction. And these 3 can be coupled, as happens when managing monitoring and punishment of free riding behaviors, which include both information and material resource processing. And now we see that abstraction is a way to reduce the coordination cost of an increasing number of parts/modules at lower levels. A new level can emerge when the costs of coordination of parts becomes equal to the benefits of synergizing these parts (which means that the costs must increase faster than the benefits with increasing part number, though they start out less at low part number), and then new proto-parts emerge, which once they become specialized modules, can be coordinated into the new higher level.

Sometimes we could also have functional levels that are evolvable.

Evolvable levels

What makes SOME entities (but not others) evolutionary levels of organization? One can have two or more individuals (or populations or statistical ensembles of individuals) that are collaborating, but they do not form an evolutionary level, unless certain resource sharing requirements are met (see our simulation and theoretical paper here for some requirements), roughly that the sharing of resources for a small, attempted new-strategies group (aka invading group) does not get completely diluted by having to equitably (based on population size alone) share resources with large, established, old-strategy populations. This is a criterion for evolvability of the highest level of organization that currently exists. It is similar to the previously discussed criterion for existence of a functional level in that it involves a constraint on how much resources can be shared outside of a group, but they are not identical (One is for an invading group, the other for an established group. One is for the highest level, the other for any level). And the former is not sufficient for keeping the evolvability of lower levels, though it is more stringent than the latter.

Evolvability involves not just a source of variation and heredity, but the ability to make copies of oneself. Theory so far suggests that each time a new evolutionary level emerges, the parts comprising it (which could have been previously evolutionary levels themselves) lose their evolvability, except in certain circumstances (which we will discuss in detail in future posts, and see below) one of which is free riding of parts. Evolutionary levels also reduce harmful-to-the-highest-level competition between their parts, increase cooperation, synergy and coordination among their parts (so capitalism is a functional, but not evolutionary level).

Keeping evolvability of lower functional levels when a new evolutionary level emerges is dangerous: those lower levels could outcompete it and destroy themselves in the process (or at least lose the benefits of synergy if the synergy has not become obligate). This is the well known case of free riding. Besides free riding, there is another possibility for evolvability of functional lower levels: it is possible mathematically to have lower level evolvability if a certain sub-group of parts (could be 1 or more) has zero net (cooperative minus competitive) interaction with the rest of the parts that comprise the higher level. If this entity was not interacting in any beneficial way with other parts, it would not be a part of a greater whole, just a competitor. So some of these interactions external to the entity, with the rest of the parts of the greater whole (higher level), have to be beneficial (to both entity and the rest of the whole) and others harmful/competitive to the that entity (and the whole). The precise conditions for how this happens is an area of active research for CARE and coincides with Civilization Research Institute's (CRI) search for the third attractor (for now equating freedom with evolvability and foresight, perhaps several levels deep). For now, the take home is that this criterion for the evolvability of a lower level, is the third and most stringent criterion we've encountered that involves resource sharing, and is similar but different from the criterion for the existence of a functional level, and the criterion for the emergence of a highest functional and evolvable level.

CRI's dystopic attractor corresponds to the standard situation where the higher level suppresses the evolvability of the lower level, and is mostly what happens in biological systems, and many social systems. The chaotic attractor is the situation where the higher functional level is not an evolutionary level and does not suppress the evolvability of the lower level, and also has too many parts to monitor and prevent free riding, sometimes destroying intermediate levels that have a manageable number of parts and can prevent free riding more effectively than if the management of free riding is left to one highest level alone.

As far as we know, evolvability of lower levels is not required for fitness of the highest level reasons, but only to satisfy our value of freedom (especially at the human individual level), which we speculate are roughly related to evolvability, especially when there are several evolvable levels involved.

The 3 types of attractors also seem to correspond to the 3 network diagrams at the beginning of this post, that show how information and resources/energy are shared among parts, within and outside of levels (these are examples, they are not unique ways of instantiating these attractors. The chaos attractor could be implemented with a random network, but we speculate that it is the constant connectivity and lack of intermediate levels that is the issue, not the randomness. Or it could be non-modularity in resource flows that leads to the chaos attractor, not shown)

How can we test these hypotheses empirically? Biology seems to be easier to do experiments in than social science...